Auf was es wirklich in der Statistik Klausur ankommt

In diesem Artikel werde ich dir zeigen, auf was es wirklich in der Statistik Klausur ankommt, um eine sehr gute Note zu schreiben. Woher ich das weiß? Mein Name ist Dr. Christoph Giehl, ich bin seit 2014 Dozent für Statistik und Methoden der empirischen Sozialforschung an verschiedenen deutschen Universitäten und habe selbst schon zahlreiche Klausuren gestellt. Ich tausche mich regelmäßig mit anderen Dozentinnen und Dozenten aus, um meine Lehre ständig zu verbessern.

Unter anderem reden wir bei solchen Gelegenheiten ebenfalls über unsere Klausuren und die Überlegungen die wir anstellen, wenn wir diese erstellen. Dabei werden wir immer wieder vor die gleichen Herausforderungen gestellt, wie ich in vielen dieser Gespräche bemerkt habe. Und natürlich reagieren viele von uns auf die gleiche Weise auf diese Herausforderungen.

Der Vorteil für dich als StudentIn besteht nun darin, dass du dich sehr viel effektiver auf deine Klausur vorbereiten kannst, wenn du diese Herausforderungen kennst und weißt, wie wir Dozierende für gewöhnlich auf diese reagieren. Hiervon leitet sich nämlich direkt ab, wie deine Klausur mit hoher Wahrscheinlichkeit aufgebaut sein wird und auf welche Aufgaben es besonders viele Punkte gibt. Lass mich dir also zeigen, auf was es wirklich in der Statistik Klausur ankommt, um eine Topnote zu kassieren.

Inhaltsverzeichnis

1. Viele Themen in kurzer Zeit
2. Berechnen komplexer Statistiken
3. Der Charm von Grafiken
4. Interpretieren ist wichtiger als Rechnen
5. Fazit und weiterführende Unterstützung

1. Viele Themen in kurzer Zeit

Wenn du nicht gerade eine Vorlesung oder ein Seminar zu einem ganz bestimmten statistischen Thema wie etwa der Regressionsanalyse besuchst, stehen die Chancen sehr gut, dass du in deiner Statistik Veranstaltung etwas zu sehr vielen verschiedenen Themenbereichen gehört hast. Dies ist zumindest in den allermeisten Einführungsveranstaltungen, wie du sie typischerweise im Bachelor-Studium besuchst, der Fall. Die verschiedenen Themenbereiche reichen dabei unter anderem von der univariaten Statistik über die multivariate Statistik bis hin zur Inferenzstatistik und schließen dabei auch oft das Zeichnen von Abbildungen und das Testen von Hypothesen mit ein. Bezeichnung wie deskriptive Statistik, deduktive Statistik und induktive Statistik sind synonyme, die du sicher auch ab und zu hörst.

Aber warum ist das nun wichtig für dich?

Im Grunde ist es ganz einfach so, dass Dozierende bei der Konzeption ihrer Klausuren gerne Fragen zu jedem dieser Themenbereiche einbauen. Wir würden unsere Studierende also am liebsten eine Kreuztabelle zeichnen und einen Chi²-Test durchführen lassen, Mittelwerte, Standardabweichungen und Pearsons r berechnen lassen, eine komplette Regressionsanalyse durchführen und vollständig (inklusive Hypothesentest) interpretieren lassen und dann noch Box-Plots, Balkendiagramme, Streudiagramme und Histogramme zeichnen lassen.

Das alles ist aber natürlich nicht in 90 Minuten (so lange geht eine Statistik Klausur in der Regel) möglich!

Was also tun? Ganze Themenblöcke raus streichen wollen wir nicht, schließlich finden wir StatistikerInnen die doch alle wichtig! Die Alternative besteht also darin, Aufgaben so zu stellen, dass deren Lösung nicht zu viel Zeit in Anspruch nimmt und am besten noch mehrere der unterschiedlichen Themenbereiche umschließt.

Ein einfaches Beispiel hierfür ist das Erstellen eines Box-Plots. Um diesen zeichnen zu können, musst du nämlich eine Häufigkeitstabelle lesen, den Median bestimmen und Quartile berechnen können. Wenn du dann noch zwei Box-Plots zeichnen sollst, können wir auch direkt nach einem Gruppenvergleich, also einer Interpretation fragen. Da ein Boxplot mit etwas Übung schnell zu zeichnen ist, haben wir somit in kurzer Zeit viele verschiedene Themenbereiche abgefragt.

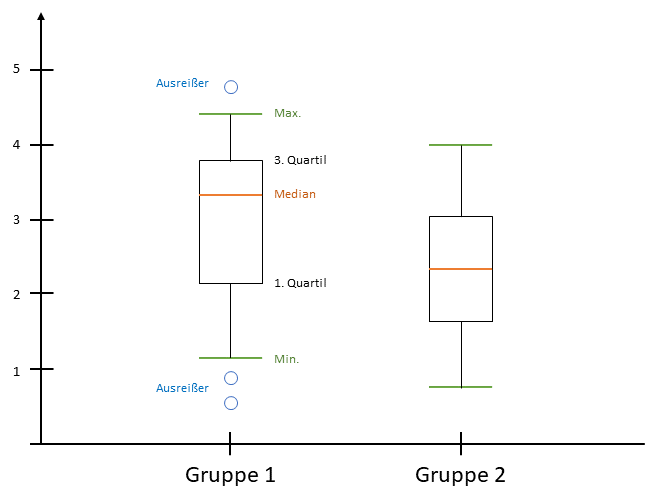
Denke auch an die persönlichen Vorlieben deiner Dozentinnen und Dozenten

Neben solchen „Drei-Fliegen-mit-einer-Klappe-Aufgaben“ haben wir Dozierenden in der Regel auch ganz bestimmte Vorlieben bei den Themenbereichen, die wir besonders wichtig finden. Und was wir besonders wichtig finden, MUSS einfach in die Klausur.

Wieder ein Beispiel: Mein eigener Doktorvater (ein Soziologe) ist ein großer Verfechter der multivariaten Regression in all ihren Formen und Farben. Dies kann man daran merken, dass er das Thema während der Vorlesung drei Wochen lang behandelt und auch ein Lehrbuch über die Regression geschrieben hat. Mindestens eine Aufgabe zur Regression kommt entsprechend in jeder Klausur. Weil es aber ziemlich lange dauern würde, eine komplette Regression berechnen zu lassen, zeigt er die Ergebnisse einer Regression und lässt diese dann interpretieren. Punkte gibt es also auf das Verstehen, nicht auf das Rechnen.

Finde also heraus, ob deine Dozentin bzw. dein Dozent ebenfalls Vorlieben für bestimmte Verfahren hat und bereite dich besonders gut hierauf vor. Daneben gibt es auch Verfahren, die innerhalb einer Fachrichtung als Standard gelten. In der Psychologie z. B. begegnet dir die ANOVA an jeder Ecke. Als Psychologie-StudentIn währe es also clever, sich besonders gut hierauf vorzubereiten.

Zwischenfazit

Überprüfe zur Vorbereitung auf deine Klausur den Lehrplan des Semesters und identifiziere die einzelnen Themenbereiche. Welche der behandelten statistischen Maßzahlen lassen sich einfach und schnell berechnen, für welche ist die Berechnung sehr Zeitaufwändig und kompliziert? Für welche der Themen brauchst du Vorwissen aus anderen Themenbereichen, so dass bei einer Frage zu einem Thema das benötigte Vorwissen direkt mit abgefragt werden kann? Welche der Themen wurden besonders intensiv behandelt und hat deine Dozentin bzw. dein Dozent Vorlieben bei bestimmten Themen?

Die Beantwortung dieser Fragen wird dir dabei helfen einzuschätzen, auf welche Themen du dich besonders intensiv vorbereiten solltest.

2. Berechnen komplexer Statistiken

Lass uns nun zu ganz konkreten Beispielen für typische Klausuraufgaben kommen. Wir gehen dabei weiterhin davon aus, dass Dozierende gerne Aufgaben wählen, die verschiedene Themenbereiche abdecken, um möglichst viel Stoff in kurzer Zeit abfragen zu können. Dieses Prinzip lässt sich nämlich hervorragend bei der Berechnung bestimmter statistischer Maßzahlen anwenden, die sozusagen „aufeinander aufbauen“. Lass mich dir an zwei Beispielen erklären, was ich meine.

Beispiel 1: Kreuztabellen und Chi²-Test

„Gegeben sei der folgende Datensatz. Berechnen Sie ein geeignetes Assoziationsmaß für den Zusammenhang zwischen den beiden Variablen ‚Arbeitslosigkeit‘ und ‚Depression‘ und begründen Sie Ihre Auswahl. Führen Sie zudem einen Signifikanztest durch und interpretieren Sie das Ergebnis.“

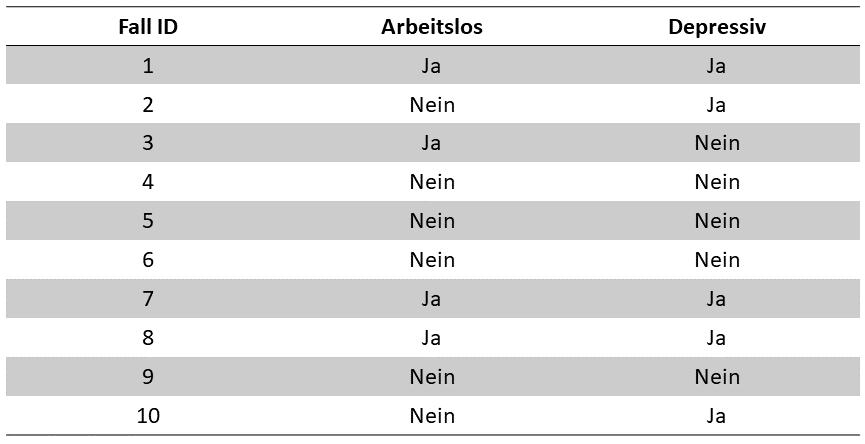
Eine Aufgabe, die so oder so ähnlich formuliert ist, findet sich wohl in den meisten Klausuren. Dies liegt daran, dass mit einer einzigen Aufgabe gleich mehrere verschiedene Themenbereiche abgedeckt werden können und alle Schritte, die zur Lösung der Aufgabe notwendig sind, aufeinander aufbauen. Die eigentliche Berechnung dauert, wenn die Aufgabe richtig gelöst wird, zudem nicht all zu lange, was PrüferInnen ebenfalls zugute kommt, wie weiter oben bereits erklärt.

Um die Aufgabe zu lösen, sind die folgenden Schritte notwendig:

1. Du musst anhand des Datensatzes erkennen, dass es sich bei beiden Variablen um sogenannte nominal skalierte, dichotome Variablen handelt. Dies ist notwendig, um das geeignete Assoziationsmaß zu bestimmen und testet dein Verständnis von Skalenniveaus. Für die korrekte Bestimmung des Skalenniveaus gibt es dann Punkte.
2. Als nächstes sollst du begründen können, dass für die Assoziation zwischen zwei nominalskalierten Variablen ein Chi²-basiertes Assoziationsmaß verwendet wird, wobei man Chi² für zwei dichotome Variablen in das Assoziationsmaß „Phi“ umrechnet. Für die korrekte Bestimmung des geeigneten Assoziationsmaßes gibt es ebenfalls Punkte.
3. Nachdem du begründet hast, welche statistischen Maßzahlen du berechnest, musst du als nächstes eine Kreuztabelle zeichnen. Auch hierauf gibt es natürlich Punkte.
4. Nun berechnest du auf Basis der Kreuztabelle zunächst Chi² und dann Phi, wobei beide korrekte Teillösungen jeweils Punkte geben.
5. Für die Bestimmung des Signifikanzniveaus musst du dann einen Chi²-Test durchführen. Für die formal korrekte Beschreibung dieses Hypothesentests gibt es Punkte, für das Ablesen des korrekten Signifikanzniveaus aus der Chi²-Tabelle ebenfalls.
6. Als letztes musst du das Ergebnis noch korrekt interpretieren. Wichtig sind hierbei die Stärke des Zusammenhangs auf Basis von Phi sowie eine genauere Beschreibung, was die Höhe des Signifikanzniveaus im Kontext der Aufgabe bedeutet, wobei beides jeweils Punkte gibt.

Du siehst also, dass das Lösen der Aufgabe aus gleich mehreren Schritten besteht, die alle aufeinander aufbauen und sehr unterschiedliches Wissen von dir erfordern. Gleichzeitig sollte die Aufgabe für gut vorbereitete Studierende in 20 bis maximal 30 Minuten zu lösen sein, so dass das Lösen der Aufgabe keinen zu großen Teil der Zeit in Anspruch nimmt. Aus Sicht von Prüferinnen und Prüfern wäre das also die „perfekte Aufgabe“.

Beispiel 2: t-Test, Pearsons r und Regression

Diese Art von Aufgabe, die eigentlich aus mehreren, aufeinander aufbauenden Teilaufgaben besteht, funktioniert nicht nur bei Chi² und dichotomen Variablen. Ebenfalls sehr beliebt sind alternativ auch die folgenden Aufgaben:

1. Gegeben sei die folgende Häufigkeitstabelle für die Variable „Einkommen der Studierenden der Vorlesung Statistik I“. Berechnen Sie das arithmetische Mittel, die Varianz und die Standardabweichung für die Variable.
2. Das mittlere Einkommen der Studierenden einer anderen Vorlesung (n = 120) beträgt 650 € (Standardabweichung = 118). Gibt es statistisch signifikante Unterschiede zwischen dem Einkommen der Studierenden aus den beiden Seminaren? Führen Sie einen vollständigen Hypothesentest durch, um die Frage zu beantworten.

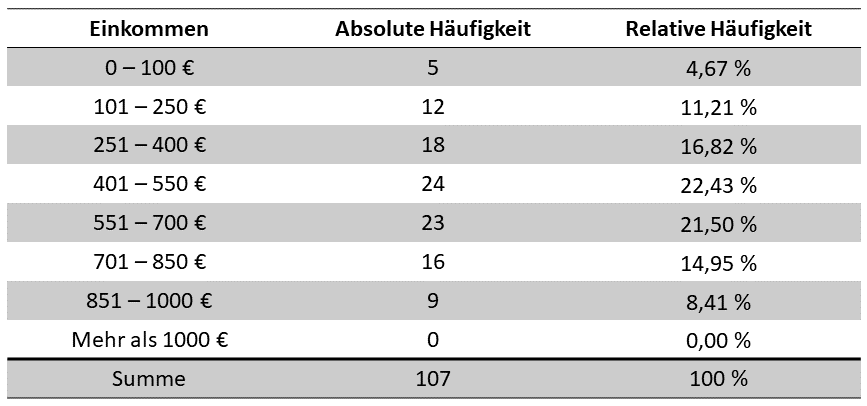
Um die beiden Aufgaben zu lösen, musst du:

1. Häufigkeitstabellen lesen können
2. Mittelwert, Varianz und Standardabweichung berechnen können
3. Die formalen Schritte eines Hypothesentests kennen
4. Einen t-Test für Gruppenunterschiede durchführen können (das Einkommen ist eine sogenannte „metrische Variable“, wobei für diese der t-Test bei der Analyse von Gruppenunterschieden genutzt wird, wenn genau zwei Gruppen existieren).

Alternative Aufgabenstellung

Statt der Berechnung des t-Tests (oder zusätzlich dazu) ist auch eine der folgenden Teilaufgaben denkbar:

3. Das durchschnittliche Alter der Studierenden der Vorlesung „Statistik I“ beträgt 20,4 Jahre (Standardabweichung = 1,8), die Kovarianz zwischen dem Alter der Studierenden und deren Einkommen beträgt 0,9. Berechnen Sie ein geeignetes Assoziationsmaß für den Zusammenhang und begründen Sie ihre Auswahl. Führen Sie zudem einen vollständigen Hypothesentest durch und interpretieren Sie das Ergebnis.

4. Berechnen Sie eine Regression vom Einkommen der Studierenden auf deren Alter. Führen Sie auch hierfür einen Hypothesentest durch und interpretieren Sie das Ergebnis.

Für diese Aufgaben müsstest du also mithilfe der Varianzen bzw. Standardabweichungen und der gegebenen Kovarianz Pearsons r, den Regressionskoeffizienten b und die Regressionskonstante a berechnen. Du musst ebenfalls die formalen Schritte eines Hypothesentests kennen und alle berechneten Koeffizienten und Signifikanzniveaus interpretieren können. Das lösen der gesamten Aufgabe sollte für gut vorbereitete Studenten aber trotzdem nicht länger als 20 bis 30 Minuten Zeit in Anspruch nehmen, da einige der relevanten, statistischen Maßzahlen bereits gegeben sind und du diese „nur noch“ an der richtigen Stelle in den entsprechenden Formeln einsetzen musst. Aus Sicht von PrüferInnen ist das also ebenfalls eine sehr gute Aufgabe.

Zwischenfazit

Die beiden Beispiele zeigen dir, dass PrüferInnen zur Lösung des weiter oben beschriebenen „Zeitproblems“ sehr gerne Aufgaben verwenden, bei denen die Lösungsschritte aufeinander aufbauen und deren Lösung gleichzeitig komplexes und vielfältiges Wissen erfordern. So lassen sich in relativ kurzer Zeit verschiedene Wissensbereiche der Statistik testen, was schließlich der Ziel jeder Klausur ist.

Natürlich gibt es noch weitere Aufgaben für die Statistik Klausur, bei denen dies möglich ist. Die beiden hier gezeigten Beispiele gehören aber definitiv zu den beliebtesten, weshalb es sich besonders lohnt, sich auf diese vorzubereiten.

3. Der Charm von Grafiken

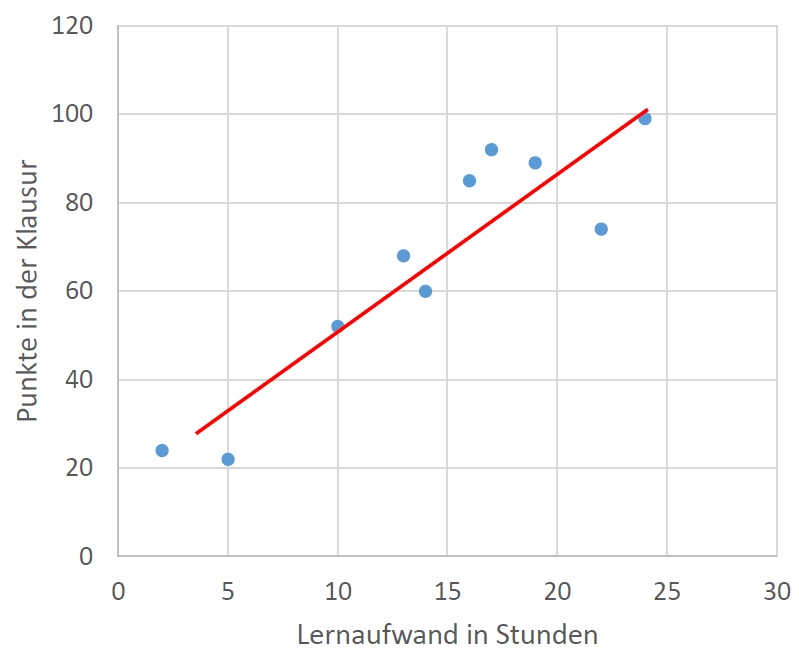
Ich habe es weiter oben schon beschrieben, möchte es aber wirklich noch einmal betonen: Das Zeichnen bzw. Interpretieren von Grafiken eignet sich ebenfalls hervorragend als Klausuraufgabe. Ebenso wie bei den Beispielen zuvor wird Wissen aus verschiedenen Teildisziplinen der Statistik benötigt, um die Aufgabe lösen zu können, während das Zeichnen und Interpretieren einer Grafik wiederum nicht allzu viel Zeit in Anspruch nimmt.

Ich habe hierfür weiter oben bereits das Beispiel „Boxplot“ aufgegriffen, für welchen du Median und Quartile berechnen musst. Auch ein Balkendiagramm bzw. ein Histogramm lässt sich noch relativ einfach zeichnen.

Eine entsprechende Klausuraufgabe würde dann etwa wie folgt lauten:

Gegeben sei die folgende Häufigkeitstabelle. Visualisieren Sie diese mit einer geeigneten Grafik, begründen Sie ihre Auswahl und interpretieren Sie das Ergebnis.

Erneut ist es also zunächst relevant, dass du das Skalenniveau der verwendeten Variablen korrekt bestimmen kannst, da sich hieraus ergibt, welche Grafik die geeignete ist. So verwendest du zum Beispiel für nominal und ordinal skalierte Variablen Balkendiagramme, für metrisch skalierte Variablen Histogramme. Boxplots lassen sich bei ordinal und metrisch skalierten Variablen anwenden und eignen sich besonders bei einem Gruppenvergleich oder bei der Gegenüberstellung von verschiedenen Variablen. Ein Streudiagramm wiederum wird gezeichnet, um die Assoziation zwischen zwei metrischen Variablen darzustellen. Eine Regressionsfunktion kann gezeichnet werden, um Koeffizient und Konstante zu visualisieren.

Natürlich gibt es noch sehr viel mehr Grafiken, diese Aufzählung soll dir nur eine Übersicht bieten. Grundsätzlich entscheidest du dich in deiner Klausur natürlich für eine Grafik, welche auch bei dir in der Veranstaltung behandelt wurde.

Daneben ist es aber auch eine sehr beliebte Aufgabe, eine fertige Grafik abzubilden und diese „nur“ interpretieren zu lassen. Dies spart noch mehr Zeit ein, erfordert aber einen sehr ähnlichen Wissensstand, um die Aufgabe korrekt lösen zu können. Generell kommt der korrekten Interpretation eine sehr hohe Bedeutung zu, wie du im nächsten Abschnitt noch erfahren wirst.

Zwischenfazit

Bereite dich ebenfalls darauf vor, Grafiken zeichnen und interpretieren zu können. Balkendiagramme, Histogramme, Boxplots, Streudiagramme und Abbildungen von Regressionsfunktionen kommen dabei wohl am häufigsten vor. Schaue dir aber natürlich vor allem an, welche Diagramme in deiner Veranstaltung behandelt wurden.

4. Interpretieren ist wichtiger als Rechnen

Hand aufs Herz: Ich habe seit meiner Statistik Klausur 2010 vielleicht noch bei einer Hand voll Gelegenheiten selbst per Hand statistische Maßzahlen berechnet. Warum auch, schließlich verwende ich genau hierfür Statistik Software wie SPSS und R?!

Auf die Frage eines Studenten, ob es für die Klausur reicht, wenn er alles rechnen, aber nicht interpretieren kann, lautete deswegen meine Antwort: „Es ist das Ziel, Wissenschaftler und keine Taschenrechner auszubilden“.

Ich persönlich gehe sogar soweit, dass für meine Klausuren eher der umgekehrte Fall gilt. Für mich würde es eher ausreichen, wenn man alles richtig interpretieren aber nicht berechnen kann. Ganz einfach weil das korrekte Interpretieren der Ergebnisse so viel wichtiger ist als das korrekte Berechnen der Ergebnisse.

Ich sage damit nicht, dass das Rechnen keine Rolle spielt. Es spielt nur eben die kleinere Rolle als das Interpretieren. Für dich hat das nun zwei Konsequenzen: Zum einen solltest du bei der Klausurvorbereitung wirklich großen Wert darauf legen zu lernen, wie du Ergebnisse richtig interpretierst. Zum anderen macht es in der Klausur wirklich Sinn, eine Aufgabe auch dann zu versuchen, wenn du mit dem Rechnen überfordert bist. Ich verspreche dir, du wirst selbst bei einer komplett falschen Rechnung noch Punkte bekommen, wenn du das falsche Ergebnis richtig interpretierst. So würden es zumindest humane PrüferInnen handhaben.

Tipps, um dir das Interpretieren zu erleichtern

Skalenniveaus verstehen

Bei der Entscheidung über das optimale Verfahren und der anschließenden Interpretation der statistischen Maßzahlen ist es zunächst mit das wichtigste zu verstehen, dass es verschiedene Arten von Variablen und Daten gibt. Aus praktischer Sicht ist dabei das „Skalenniveau“ das wohl wichtigste Unterscheidungskriterium.

Vereinfacht gesagt bestimmt das Skalenniveau, welche Rechenoperation mit einer Variable gemacht werden darf. Lass dich von den mathematischen Formulierungen aber nicht einschüchtern, im Grunde ist es ganz einfach:

Nominal skalierte Variablen

Zunächst gibt es sogenannte nominale oder ungeordnet-kategoriale Variablen. Bei solchen Variablen lassen sich die einzelnen Ausprägungen einer Variable zwar klar voneinander unterscheiden, die Ausprägungen lassen sich jedoch nicht sinnvoll nach einer bestimmten Hierarchie sortieren. Ein Beispiel für eine nominale Variable ist die Nationalität. „Deutsch“ ist etwas anderes als „Französisch“, es ist jedoch nicht „mehr“ oder „weniger“, „besser“ oder „schlechter“ etc. Ein anderes Beispiel ist das Geschlecht. Auch hier lassen sich zwar „Männlich“, „Weiblich“, „Divers“ etc. unterscheiden, nach Maßstäben wie „mehr“ oder „weniger“ bzw. „besser“ oder „schlechter“ lassen sich die einzelnen Ausprägungen jedoch nicht sortieren.

Ordinal skalierte Variablen

Dies ist anders bei ordinalen bzw. geordnet-kategorialen Variablen. Hier ist es nämlich möglich, die einzelnen Ausprägungen der Variable zu sortieren. Was bei diesen Variablen jedoch nicht funktioniert ist, die Distanzen zwischen den einzelnen Ausprägungen eindeutig zu quantifizieren. Ein klassisches Beispiel hierfür ist der Schulabschluss. Abitur ist „mehr“ als ein Realschulabschluss (welcher wiederum „mehr“ als ein Hauptschulabschluss ist), das Abitur stellt einen „höheren“ Schulabschluss dar und gilt gemeinhin als „besser“. Es existiert jedoch keine exakte Quantifizierung davon, wie viel „besser“ das Abitur ist.

Metrisch skalierte Variablen

Um die exakte Distanz zu quantifizieren, müssten wir uns statt dem Schulabschluss zum Beispiel die Dauer des Schulbesuches in Jahren anschauen, also eine eindeutig metrische Variable. Bei metrischen Variablen verhält es sich im Gegensatz zu ordinalen Variablen nämlich so, dass die exakten Distanzen zwischen den einzelnen Ausprägungen bestimmt werden können. Ein Mensch, der 12 Jahre zur Schule gegangen ist, hat die Schule 3 Jahre länger besucht als ein Mensch, der 9 Jahre zur Schule gegangen ist. Weitere Beispiele für metrische Variablen sind das Alter und das Einkommen.

Streng genommen werden metrische Variablen noch in intervall- und ratioskalierte Variablen unterteilt. Diese Unterscheidung ist für die Auswahl derjenigen statistischen Maßzahlen, welche im Statistik Grundstudium behandelt werden, jedoch unerheblich. Quer dazu gibt es noch die Unterscheidung zwischen diskreten und kontinuierlichen Variablen. Aber auch diese ist aus praktischer Sicht lediglich bei komplexeren Verfahren relevant.

Wertebereiche verstehen

Häufig unterschätzt, jedoch ebenfalls sehr wichtig für die korrekte Interpretation von Ergebnissen ist der Wertebereich einer Variable. Als Wertebereich wird dabei der Bereich aller „erlaubten“ Werte einer Variable bezeichnet. Sagen wir mal als Beispiel, dass eine Variable die Zustimmung zu einer bestimmten Aussage auf einer Skala von 1 bis 5 misst, wobei 1 für „komplette Ablehnung“ und 5 für „komplette Zustimmung“ steht. Die entsprechende Variable hat dann einen Wertebereich von 1 bis 5.

Hätten wir für diese Variable dann einen Mittelwert über alle Befragte von exakt 4, dann würde das bedeuten dass die Befragten der Aussage eher zustimmen. Bei einem Mittelwert von 2 würden die Befragte die Aussage im Schnitt eher ablehnen.

Das klingt banal, ich weiß. Allerdings wird die Interpretation der Ergebnisse im Kontext des Wertebereichs der Variable tatsächlich oft einfach in den Klausuren vergessen. Ich halte es nicht für unwahrscheinlich, dass dies eben genau an der scheinbaren Banalität liegt.

Neben diesem einfachen Anwendungsbeispiel ist der Wertebereich aber auch bei der Interpretation von weiterführenden Verfahren wie etwa bei t-Tests und bei Regressionen von hoher Bedeutung.

Eine Differenz zwischen zwei Gruppen von beispielsweise 1,2 mag bei einem t-Test zwar statistisch signifikant sein, bei einem Wertebereich von 1 bis 5 hat eine Differenz von 1,2 jedoch eine ganz andere Bedeutung als beispielsweise bei einem Wertebereich von 1 bis 1000. Bei einem Wertebereich von 1 bis 5 entspricht dies nämlich ganzen 24% der gesamten Antwortskala, bei einem Wertebereich von 1 bis 1000 sind es hingegen nur 0,12%. Die Differenz im zweiten Beispiel ist dann zwar vielleicht statistisch Signifikant, jedoch trotzdem sehr gering. Dies sollte bei der Interpretation der Ergebnisse auf jeden Fall berücksichtigt werden.

Standardisierte Koeffizienten verstehen

Zum Glück für dich gibt es in der Statistik einige Maßzahlen, bei denen der Wertebereich immer zwischen 0 und 1 bzw. zwischen -1 und +1 liegt. Solche Maßzahlen werden als standardisierte Koeffizienten bzw. Assoziationsmaße bezeichnet. Beispiele hierfür sind für nominal skalierte Variablen die Chi²-basierten Assoziationsmaße Phi und Cramér’s V (Wertebereich von 0 bis 1), für ordinal skalierte Variablen die Assoziationsmaße bzw. Korrelationskoeffizienten Tau a, Tau b und Tau c sowie Somers‘ d und für metrische Variablen der Korrelationskoeffizient Pearson’s r. Daneben lassen sich auch Regressionskoeffizienten von ihrer unstandardisierten Form in standardisierte Koeffizienten umrechnen.

Das besondere an standardisierten Koeffizienten ist, dass sie relativ einfach zu interpretieren sind. Ein Wert von 0 steht immer für überhaupt keinen Zusammenhang, ein Wert von 1 steht immer für einen perfekten Zusammenhang. Werte unter 0,2 wären dann also eher schwache Zusammenhänge oder Korrelationen, Werte bis 0,4 sind moderate Korrelationen während Werte ab 0,4 schon als starke Korrelationen gelten (bitte beachte, dass das Daumenregeln sind).

Hinzu kommt dann (außer bei den Chi²-basierten Assoziationsmaßen) noch das Vorzeichen. Ist der Koeffizient positiv, dann steht das für einen positiven Zusammenhang (desto höher der Wert der einen Variable, desto höher der Wert der anderen Variable). Ist der Koeffizient negativ, so steht das für einen negativen Zusammenhang (desto höher der Wert der einen Variable, desto geringer der Wert der anderen Variable).

Signifikanzniveaus verstehen

Kommen wir zuletzt zur korrekten Interpretation von Signifikanzniveaus, da diese in der Regel als das entscheidendste Kriterium beim Testen von Hypothesen gelten.

Grundsätzlich ist das Signifikanzniveau (in der Regel mit einem „p“ benannt) als Prozentwert zu verstehen, wobei du den Wert, der da als Signifikanzniveau steht, mit hundert multiplizierst, um den Prozentwert zu erhalten. Das bedeutet, dass ein p-Wert von 0,05 einem 5% Signifikanzniveau entspricht (0,05 * 100 = 5). p = 0,01 entspricht dann 1%; p = 0,25 entspricht 25% usw.

Im Detail sagt dieser Prozentwert nun aus, wie wahrscheinlich es ist, dass deine Hypothese doch nicht stimmt. Aber was heißt das nun genau? Sagen wir mal als Beispiel, dass du die Hypothese überprüfen willst, dass Studierende im ersten Mastersemester über ein höheres Einkommen verfügen als Studierende im ersten Bachelorsemester. Du würdest dann zunächst die Differenz der Einkommens-Mittelwerte der beiden Gruppen berechnen und würdest hierbei dann zum Beispiel herausfinden, dass MasterstudentInnen im Schnitt 120 € mehr verdienen als BachelorstudentInnen.

Damit ist deine Hypothese jedoch nicht bestätigt! Es ist nämlich möglich, dass in deiner Stichprobe rein zufällig besonders viele „reiche“ MasterstudentInnen und besonders viele „arme“ BachelorstudentInnen gelandet sind. Der Einkommensunterschied wäre dann auf einen blöden Zufall bei der Datenerhebung und nicht auf einen tatsächlichen Fakt zurückzuführen.

Um einen solchen „blöden Zufall“ auszuschließen, führen wir also zusätzlich einen t-Test durch und erhalten einen p-Wert von beispielsweise 0,001. Dies bedeutet dann, dass die Wahrscheinlichkeit eines solchen „blöden Zufalls“ lediglich bei 0,1% liegt.

Hier noch eine kleine Spitzfindigkeit: Auch jetzt ist unsere Hypothese noch nicht bestätigt, sondern lediglich „vorläufig akzeptiert“. Dies liegt daran, dass die moderne Wissenschaft nach dem Paradigma des sogenannten „kritischen Rationalismus“ arbeitet, nachdem wir niemals absolute Sicherheit erlangen können, sondern immer nur ausschließen können, was nicht „der Wahrheit“ entspricht. Ein Hypothesentest ist also streng genommen der Versuch, eine Hypothese zu wiederlegen. Gelingt dies nicht, wird sie vorläufig akzeptiert. Mit dieser Formulierung („Hypothese vorläufig akzeptiert“ statt „Hypothese bestätigt“) zeigst du in deiner Klausur ein besonders tiefes Verständnis von Signifikanzniveaus und Hypothesentests.

Zwischenfazit

Der korrekten Interpretation deiner statistischen Ergebnisse kommt eine enorme Bedeutung zu. Mir als Dozent und Prüfer ist das richtige Interpretieren sogar wichtiger als das richtige Rechnen. Hier eine Zusammenfassung, auf was du unbedingt bei der Interpretation achten solltest:

• Identifiziere das Skalenniveau der Variablen und benenne es wenn du begründen sollst, warum du dich für ein bestimmtes Verfahren entschieden hast.
• Berücksichtige den Wertebereich der Variablen bei der Interpretation. Bei Mittelwerten hilft dir der Wertebereich dabei einzuschätzen, ob in der Stichprobe eine Tendenz hin zu einem bestimmten Wert vorliegt. Bei der Analyse von Gruppenunterschieden hilft der Wertebereich dabei, die Höhe des Unterschiedes zu beschreiben. Bei Regressionsanalysen hilft der Wertebereich dabei, die stärke der Effekte zu beschreiben.
• Beschreibe bei Korrelationen/Assoziationen und Regressionskoeffizienten immer die Stärke (auf Basis der standardisierten Koeffizienten), die Richtung (auf Basis des Vorzeichens) und die Signifikanz (auf Basis des p-Wertes) der Effekte.

5. Auf was es wirklich in der Statistik Klausur ankommt: Fazit und weiterführende Unterstützung

Die Klausur in Statistik zu meistern oder zumindest zu überleben stellt eine große Hürde im Leben vieler StudentInnen dar. Umso größer ist die Freude, wenn die Klausur schließlich bestanden ist.

Damit dieses Ziel auch für dich in greifbare Nähe rückt, habe ich dir in diesem Artikel die wichtigsten Tipps und Erkenntnisse zum Bestehen der Statistik Klausur zusammen gefasst, die mir in meiner Laufbahn als Dozent für Statistik und Methoden der empirischen Sozialforschung begegnet sind.

Ich habe dir gezeigt, welche Überlegungen ich und viele andere DozentInnen bei der Planung der Klausur anstellen und welche typischen Klausuraufgaben sich hieraus ergeben. Wenn du verstehst, was uns DozentInnen wirklich wichtig ist, welche Aufgaben wahrscheinlich dran kommen und nach welchen Kriterien wir Punkte vergeben, steht einer optimalen Vorbereitung nichts mehr im Weg.

Jetzt hängt es nur noch von dir ab. Schnapp dir am besten sofort deinen Semesterplan und überprüfe, welche Themenbereiche in diesem Semester besonders wichtig waren. Schaue nach, ob deine DozentIn ein bestimmtes statistisches Verfahren präferiert und bereite dich auf dieses Verfahren besonders gut vor. Das kannst du einfach herausfinden, in dem du dir die Publikationen deiner DozentIn anschaust. Lerne, Abbildungen zu zeichnen und zu interpretieren. Lerne sowieso, wie die einzelnen Maßzahlen interpretiert werden sollten. Und vergiss natürlich trotzdem nicht das Rechnen. Was wäre Statistik schließlich ohne Mathe 😉

In meinem Blog und der Ressourcenseite für Studierende habe ich dir weitere hilfreiche Tipps und Tricks zusammengefasst, die du für die Vorbereitung auf die Klausur in Statistik verwenden kannst. Schaue dort gerne mal vorbei. Lass mir auch gerne ein Kommentar auf dieser Seite da, falls du Fragen hast oder dir einen weiteren Blogartikel zu einem bestimmten Themenbereich wünschst. Dafür kannst du natürlich auch gerne das Kontaktformular auf dieser Seite verwenden.

Ich wünsche dir ganz viel Erfolg bei deiner Statistik Klausur.

Mit besten Grüßen,

Dr. Christoph Giehl